Table of contents
- What are Rational Numbers?
- Difference between Rational Numbers and Fractions
- Symbol for Rational Numbers
- Examples of Rational Numbers
- Examples of Numbers which are not Rational Numbers
- Types of Rational Numbers
- Rational and Irrational Numbers
- Difference between Rational and Irrational Numbers
- Operations with Rational Numbers
- Addition of Rational Numbers
- Subtraction of Rational Numbers
- Multiplication of Rational Numbers
- Division of Rational Numbers
- Solved Examples
- Practice Questions
- Frequently Asked Questions
Rational numbers is a foundational concept in the realm of mathematics. The term "rational" is derived from "ratio," underlining its connection with fractions that represent ratios. Let us explore the world of rational numbers.
What are Rational Numbers?
Rational numbers are numbers expressed in the form \frac{p}{q} where p and q are integers and p\neq q. They encompass various types of numbers, such as natural numbers, whole numbers, integers, fractions of integers, and decimals. They are integral to our mathematical world, as most of the numbers we encounter daily fall under this category. Every integer, whole number, natural number, and fraction is a rational number, though the reverse is not always true.
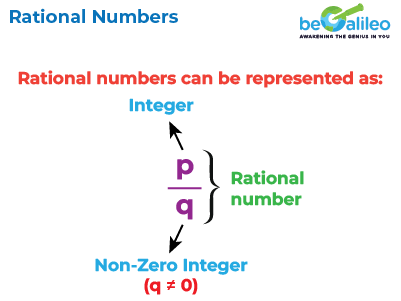
Difference between Rational Numbers and Fractions
Fractions have only whole numbers as their numerator and denominator (with the denominator 0). Whereas, Rational Numbers can have integers for both numerator and denominator.
Symbol for Rational Numbers
The collection of rational numbers is symbolized as Q. It'simportant to recognize that rational numbers encompass natural numbers, whole numbers, integers, and decimals.
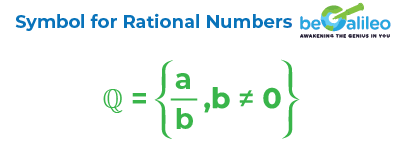
Examples of Rational Numbers
A glimpse into the world of rational numbers:
- 46: Expressible as \frac{46}{1}.
Every natural number can be written as a rational number with denominator as 1 - -3: Expressed as \frac{-3}{1}.
Every integer can be written as a fraction with 1 as the denominator. - 0: Can be denoted as \frac{0}{1}, \frac{0}{-2}, \frac{0}{35}.
0 can be written as a fraction with a non-zero denominator. - \sqrt{4}=2: Square roots of perfect squares are rational.
- \frac{-2}{3}: Negative fractions are rational.
- 0.2 or\frac{2}{10}: Both decimal and fractional formats are rational.
- \frac{15}{99}: Rational fractions, simplifiable.
Examples of Numbers which are not Rational Numbers
Certain numbers don't adhere to rationality. Take the case of square roots, cube roots, etc., of natural numbers, where exact values elude us. Such numbers are not rational numbers. Examples: \sqrt{2},\sqrt[3]{5} ,\sqrt{7} ,2\sqrt{3} : etc.
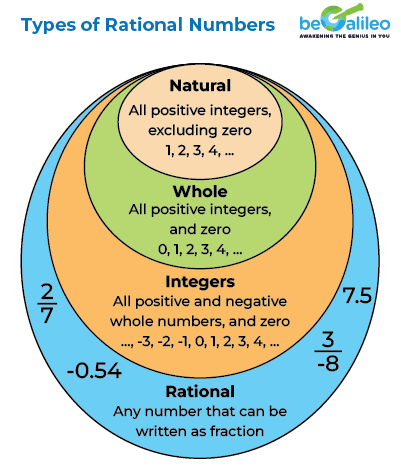
Types of Rational Numbers
Rational numbers come in several forms. The different types of rational numbers are given below:
- Integers: -2, 0, and 5.
- Fractions: e.g., \frac{2}{7},\frac{-2}{3}.
- Terminating Decimals: Such as 0.35, 0.667.
- Non-terminating Decimals with Repetitive Patterns: e.g., 0.222…, 0.141414…
Rational and Irrational Numbers
Numbers that aren't rational are irrational, such as\sqrt[3]{2}, π (pi) are called Irrational numbers.. Rational numbers include terminating and non-repeating decimals, while irrationals lack repeating patterns or accurate values. Do note that the sum of rational and irrational numbers is irrational.
Difference between Rational and Irrational Numbers
The key differences between rational and irrational numbers are listed in the table below.
| Property | Rational Numbers | Irrational numbers |
|---|---|---|
| Expressible as Ratio | Yes | No |
| Nature of Decimal | Finite / Recurring | Non-terminating / Non-repeating |
| Form as fraction | Yes | No |
| Examples | 4, 9,\sqrt{25} | \sqrt{2},\sqrt{3} |
Operations with Rational Numbers
Manipulating rational numbers via arithmetic operations is a fundamental skill in mathematics. Understanding these operations—addition, subtraction, multiplication, and division—enables you to solve a variety of sums and scenarios.
Addition of Rational Numbers
Addition allows us to merge rational numbers, just as we combine quantities in real life. These are the 2 rules for addition of rational numbers
- When the denominators of the given rational numbers are equal, we add the numerators and keep the denominators the same.

- When the denominators of the given rational numbers are different, we first make them equal by finding the equivalent rational number using the concept of LCM (least common multiple). Once, the denominators are equal, we add the numerators and retain the denominator.
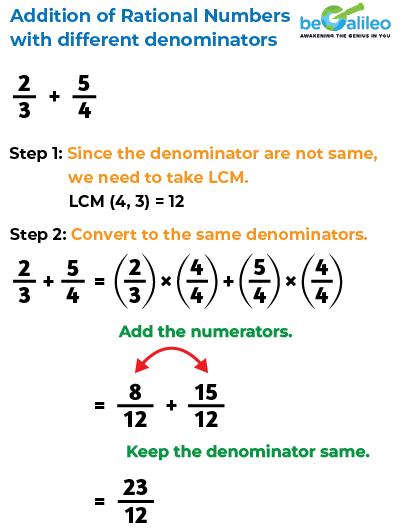
Subtraction of Rational Numbers
Subtraction helps us to find the difference between rational numbers. Similar to addition, rational numbers must share a common denominator for accurate subtraction. The rules for subtraction of rational numbers are similar to addition.
- When the denominators of the given rational numbers are equal, we subtract the numerators and keep the denominators the same.

- When the denominators of the rational numbers are not the same, we start by making them equal. This is done by finding equivalent fractions using the LCM (least common multiple). Once the denominators are the same, we can then subtract the numerators while keeping the denominator unchanged.


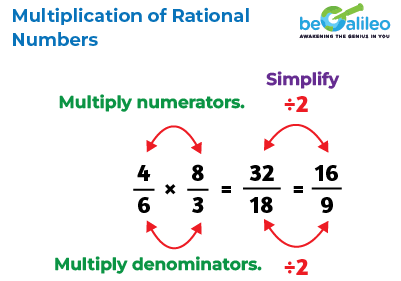
Multiplication of Rational Numbers
Multiplication is the easiest of the four arithmetic operations. To multiply two rational numbers, you multiply the numerator of the first number by the numerator of the second number, and you also multiply the denominator of the first number by the denominator of the second number.
Division of Rational Numbers
Division helps us in sharing quantities fairly among rational numbers. We know that the number which is to be divided is called the dividend and the number by which it is divided is called the divisor. To divide a rational number by another rational number, we multiply the first rational number (dividend) by the reciprocal of the second rational number (divisor).
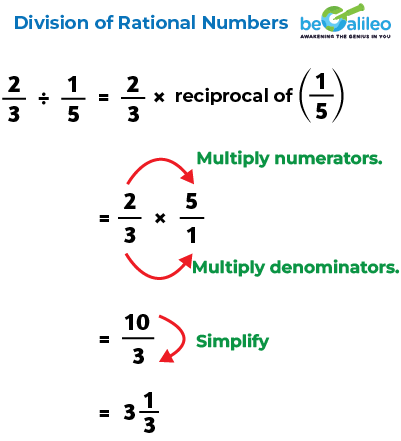
Fun Fact: Infinite Surprises of Non-Terminating Decimals
Ever wondered about numbers that never seem to settle down? Non-terminating decimals, like 0.333... or 0.141414..., keep going forever without repeating the exact same sequence. What's intriguing is that these seemingly endless patterns can actually be tamed into rational numbers. For example, 0.333... can be expressed as \frac{1}{3}, revealing the magic behind the numbers' infinite dance. It's like catching a glimpse of the endless possibilities hidden within the mathematical universe!
Solved Examples
Q1. Use the diagram to select the correct answer. Which of the following is a rational number as well as an integer?
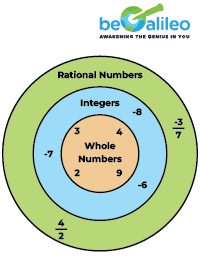
Solution:
The correct answer is b) \frac{4}{2}
All integers are rational numbers but not all rational numbers are integers. We can say, \frac{-3}{7} , \frac{4}{7},and \frac{-3}{7} , \frac{8}{18} are not integers as we cannot simplify the numerator and the denominator.
\frac{4}{2} = 2. Hence \frac{4}{2} rational number as well as an integer.
Q2. Choose True or False. 1 lies between \frac{9}{21} and 1\frac{1}{2} .
Solution:
The correct answer is a) True.
We know
\frac{9}{21} > 0 and 1 < 1 \frac{1}{2}
So,\frac{9}{21}<1 <1 \frac{1}{2}
Hence, the given statement is correct.
Q3. Find the sum of two rational numbers \frac{3}{4} and\frac{2}{3}.
Solution:
The correct answer is c) 1\frac{5}{12}
Since the denominators are not the same, we need to take L.C.M in order to convert the denominators the same. L.C.M (4, 3) = 12
\frac{3}{4}+\frac{2}{3} =(\frac{3}{4}) \times (\frac{3}{3}) + (\frac{4}{4})
=\frac{9}{12}+(\frac{8}{12})
=\frac{(9+8)}{12}
=\frac{17}{12}
=\frac{(15)}{12}
Q4. The number line shows an unknown number r. Is \frac{-r}{5}+5 positive or negative?
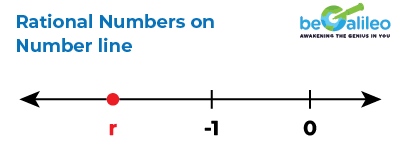
Solution:
From the number line, we can see that r is negative. Hence (-r) is positive.
\frac{-r}{5}is positive.
Therefore, \frac{-r}{5}+5is also positive.
Q5. The product of two rational numbers is \frac{-12}{25} . If one of them is \frac{21}{4} . Which of these is the other number?
Solution:
The correct answer is c)\frac{-16}{175}
Let one of the rational numbers be a.
It is given that,
a \times\frac{21}{4}=\frac{-12}{25}
By the property of reciprocals,we get
a \times \frac{21}{4}\times \frac{4}{21}=\frac{-12}{25}\times\frac{4}{21}
\Longrightarrow a=\frac{(-12)\times4}{25\times 21}
=\frac{-16}{175}
Hence, option (d) is correct.
Practice Problems
FAQs - Rational Numbers
What are rational numbers and how are they different from fractions?
Rational numbers are those that can be expressed in the form \frac{p}{q} where p and q are integers, with a non-zero denominator. While fractions are a specific type of rational numbers and can have only natural numbers as numerator and denominator, rational numbers also encompass integers and decimals, extending beyond just fractional forms.
Can whole numbers and decimals be rational numbers too?
Absolutely. Rational numbers include a wide range of numbers, such as whole numbers like 5 or -12, as well as decimals like 0.75 or -2.4. Essentially, if a number can be expressed as a fraction of integers, it's a rational number.
How do we identify a rational number?
To identify a rational number, check if it can be expressed as a fraction \frac{p}{q}, where p and q are integers and q is not zero. This encompasses whole numbers, integers, and decimals that can be written as fractions.
What's the connection between rational numbers and ratios?
The term "rational" is derived from "ratio," highlighting the connection between rational numbers and ratios. Rational numbers represent the relationship between two quantities, expressed as a fraction, and ratios are fundamental to understanding this concept.
Is 0 a rational number?
Zero is a rational number as it can be written as \frac{0}{1} (\frac{p}{q} from) where q could be non-zero.
Is pi a rational number?
Pi is not a rational number as its exact value is 3.141592653589793238. This is a non-terminating and non-recurring number. When we round off the value of pi to 3.14 then it becomes a rational number since it becomes terminating.
Can the denominator of a rational number be zero?
Denominator of a Rational number can never be zero.
Is 1 a rational number?
Yes, 1 is indeed a rational number. It can be expressed as the fraction \frac{1}{1}, where both the numerator and the denominator are integers, and the denominator is not zero. This fits the definition of a rational number, making 1 a member of this category.
















