Decimals

Decimals are a numerical representation that enables us to express numbers with both whole and fractional parts. They are a fundamental concept in mathematics and play a crucial role in various applications, from everyday calculations to complex scientific and financial analysis.

The word "decimal" is derived from the Latin word "decimus," which means "tenth." The origin of this term aligns with the foundational principles of the decimal system, which finds its basis in the concept of powers of 10.

Definition of Decimal Numbers

In the number system, decimals are used to express a part of a whole number. It is similar to fractions in concept, but with a different way of representation.

A decimal number has two parts - the whole number part and the fractional part which are separated from each other with a decimal point.

The following figure shows the parts of a decimal number.

In some cases, decimal numbers might not have a whole number part, such as when the number is less than 1.

History of Decimal Numbers

The history of decimals is a fascinating journey that spans thousands of years and involves the contributions of various cultures and civilizations. Decimal numbers started to become more common in mathematical writings during the 16th century. Simon Stevin, a mathematician from Flanders, played a key role in promoting decimal fractions through his book "Decimal Arithmetic," published in 1585.

Decimal Point Notation was introduced by John Napier in his work "Mirifici Logarithmorum Canonis Descriptio" (1614).

The Indian numeral system, including the use of zero, greatly influenced the development of modern decimal notation by The Indian mathematician and astronomer Aryabhata.

Decimal Place Value Chart

A place value chart is a very useful tool in understanding the value of the digit based on its place on the number.

For the decimal number, the whole part of the decimal which is to the left of the decimal point, follows the usual place value table.

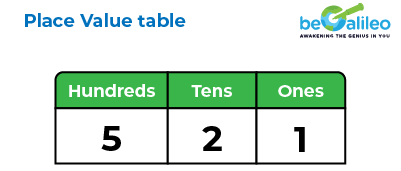
In the place value table, we know that as we move towards the left, each position is 10 times smaller.

But what happens when we reach the ones place?

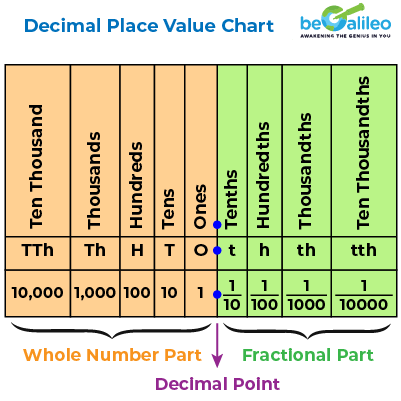
We continue the same process and the next place value is \frac{1}{10}, \frac{1}{100},\frac{1}{1000} and so on.. The decimal point is added in the place value table to separate the whole from the fractional part. It is very important in reading the decimal number.

The table below summarizes the decimal place value system. The place values to the left of the decimal point include ones, tens, hundreds, thousands, and so on. To the right of the decimal point, the place values include tenths, hundredths, thousandths, and so forth.

Expanded Form of Decimals

The expanded form of the decimal number shows the sum of place values for each digit. Decimal numbers can be expressed in expanded form using the place-value chart.

To write the decimals in an expanded form, we have to multiply each digit by its place value and add these values together.

How to Read Decimal numbers?

Reading decimal numbers is similar to reading whole numbers, with the additional step of recognizing and interpreting the decimal point.

The easiest way to read decimal numbers is to read the whole number as we would read any whole number and add “point” for decimal point and then read out each digit after the decimal point one by one.

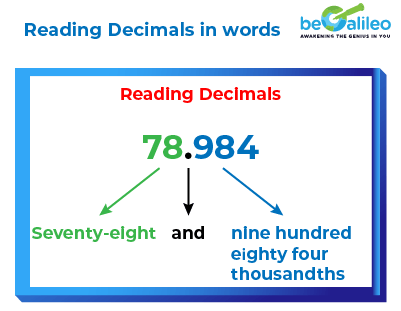
For example, 78.984 is read as “Seventy-eight point nine eight four”.

But this is an informal way of reading decimals. The more formal way of reading decimals is to read the whole number as a whole number, then add "and" for the decimal point, and read the fractional part as a whole number, followed by the place value of the last digit.

For example, in the number, 78.984, the place value of the last digit 4 is thousandth. So, the number is read as “Seventy-eight and nine hundred eighty four thousandths”.

Zero Handling: When there are leading zeros in the decimal part, they are generally ignored.

For example, 0.007 is read as "seven thousandths."

Decimals on a Number Line

Decimals can be represented on a number line just like whole numbers. A number line is a visual representation of numbers where each point corresponds to a specific value.

The number line divides the whole number into tenths, hundredths or thousandths and so on.

For example:

The number line is divided into tenths from zero to 1 in steps of 0.1.

Types of decimals

1) Based on the types of digits that follow the decimal point, decimals are divided into different categories.

• Like decimals

If two decimals have exactly the same number of digits following the decimal point, the decimal numbers are said to be "like" decimals.

For example, the decimals 4.76 and 1.12 are Like decimals because they both include two digits following the decimal point.

• Unlike decimals

If two decimals have different numbers of digits following the decimal point, the decimal numbers are said to be "Unlike" decimals.

For example, the decimals 4.766 and 1.12 are unlike decimals because both have different numbers of digits following the decimal point.

2) Depending on the type of digits that follow the decimal point, decimals can be categorized as repeating, non-recurring, or terminating decimals.

• Terminating Decimals:

A terminating decimal has a finite number of digits after the decimal point. The digits in a terminating decimal don't repeat and simply end after a certain point. These decimals can be easily converted into fractions, making calculations and comparisons straightforward.

For example:

Decimal representation of the fraction \frac{1}{4} is 0.25. So, 0.25 is a terminating decimal.

• Non-Terminating Decimals:

Non-terminating decimals continue indefinitely and do not end at a certain point. There are two types of non-terminating decimals:

• Recurring Decimals: These decimals have a repeating pattern of digits after the decimal point.
  For example: \frac{1}{3} = 0.333..., a recurring decimal that has 3s repeating indefinitely.
• Non-Recurring Decimals: These decimals continue without any repeating pattern.
  For example: \sqrt{2} = 1.4142135623…, a non-recurring decimal that goes on indefinitely without repeating a specific set of digits.

Comparison of Decimals

When comparing decimals, it's important to consider the appropriate decimal place and establish which decimal is greater, which is smaller, or if they are equal. This process involves analyzing the digits before and after the decimal point.

• If the whole number parts of the decimals are different, the decimal with the larger whole number is usually the larger decimal.

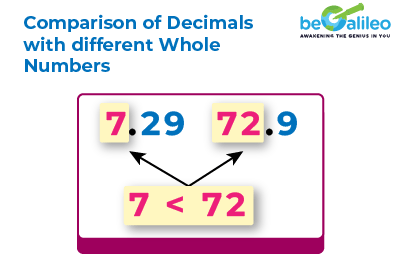
• If the whole number parts of the decimals are the same, compare the tenths place. If they are the same, then go to the next place value.

• Continue comparing the digits in each place value till you reach the end of the decimal number.

Usually, aligning the decimal points of the decimals being compared helps with a digit-by-digit comparison.

Use of Decimals in Real World

Decimals are widely used in the real world across various fields such as money, measurements, and scientific calculations due to their ability to represent numbers more precisely than whole numbers.

Here are some common applications of decimals in real-world contexts:

• Money and Finance : Decimals are fundamental for representing and calculating monetary values. They allow us to handle fractions of currency units accurately, for personal budgets, financial transactions, or investment calculations.
• Measurements : Decimals are essential in various measurement systems to represent fractions of units. For example, in the metric system, millimeters, centimeters, and meters are all based on decimals.
• Cooking and Recipes : Many recipes involve measurements in fractions, such as \frac{1}{2} cup or \frac{1}{4} teaspoon. Decimals allow cooks to make precise measurements for ingredients, leading to better culinary outcomes.
• Geography and Cartography : Maps and geographical coordinates often use decimals to represent latitude and longitude. This allows for precise location identification on Earth's surface.
• Time Calculations : Time calculations involving hours, minutes, and seconds can be expressed as decimals.
• Retail and Sales : Decimal-based pricing allows retailers to set accurate prices for products and calculate discounts more precisely.

In all these scenarios, decimals enable us to handle the complexities of modern life, ensuring precision, reliability, and informed decision-making. They help us understand things better and make smart choices. So, decimals play an integral role in shaping our understanding of the world.

Math Facts

• Between any two whole numbers, there are infinite decimal numbers.
• Every fraction is a decimal but not every decimal is a fraction.
• The winners and runners in the Olympics are determined by a minor variance in digits after the decimal point in the time.
• Different countries use distinct symbols for separating the integer and decimal parts.
  Example:
  Taiwan and Singapore - 23·89
  European countries - 23,89
  
• Decimals can be used to represent any number raised to power 10.
• Decimal Days: A decimal day consists of 10 hours, each lasting 100 minutes, and each minute containing 100 seconds.
• Some people celebrate "Decimal Day" on different dates, commemorating the adoption of decimal-based currency.