Table of contents
- What is a Fraction
- Parts of a Fraction
- Fraction of a Whole
- Fraction of a Collection
- Fractions on a Number Line
- Types of Fractions
- Proper Fractions
- Improper Fractions
- Mixed Fractions
- Unit Fractions
- Like Fractions
- Unlike Fractions
- Equivalent Fractions
- Real-world Application of Fractions
- Solved Examples
- Practice Problems
- Frequently Asked Questions
In everyday situations, there are many instances where we need only a part of something and not the entire object. For example, this happens when we share a pizza, cut a cake, or eat an apple. In the world of math, we need numbers to show these parts, and this is where the concept of fractions comes into play.
What is a Fraction?
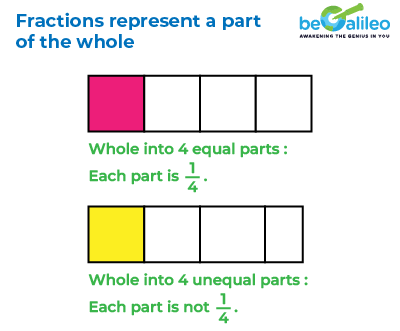
Fractions represent a part of the whole, where the whole can be an object or a collection. For writing a fraction, it is necessary that all parts of the whole are equal.
Fraction is derived from the Latin word 'fractio,' meaning 'to break,' as fractions represent how something is divided. Imagine dividing a pizza into slices; each slice is a fraction of the whole pizza.
The ancient Egyptians were the trailblazers of fractions. They used fractions in practical situations such as sharing food and resources. Their understanding of fractions paved the way for the mathematical concept we know today.
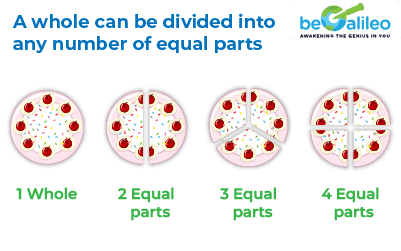
To gain a clearer perspective on fractions, let's examine the example given below. We can partition the whole into any number of equal parts. Each part signifies a fraction of the complete whole.
A whole can be divided into any number of equal parts and each part is a fraction of the whole.
Parts of a Fraction
A fraction has two parts: the numerator and denominator, which are separated by a horizontal line called a fraction bar.

The number written above the fraction bar is called the Numerator. The numerator signifies how many equal parts of the whole or collection are taken.
The number below the fraction bar is called the Denominator. The denominator signifies the total number of equal parts the whole is divided into or the total number of the same objects in a collection.
Take the example of the cake divided into 4 equal parts.
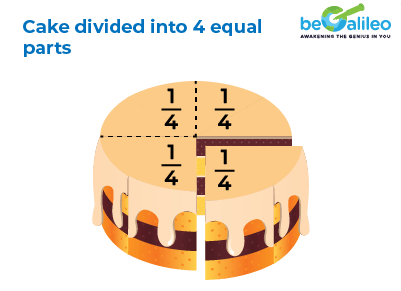
If we take one part of the cake, then it can be expressed as\frac{1}{4} and if we take 3 parts of the cake, then it is expressed as \frac{3}{4}.
Fraction of a Whole
Fractions of a whole tell us how many parts of a whole we talk about.
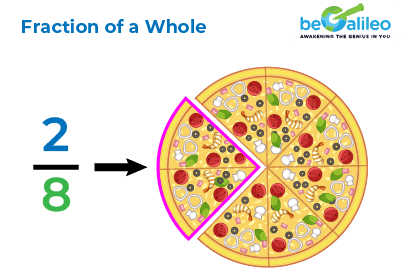
Imagine we have a delicious pizza in front of us, cut into eight equal slices. Each slice represents a fraction of the whole pizza. If we take two slices, we are essentially enjoying \frac{2}{8} of the entire pizza. In this scenario, the whole pizza serves as the reference point, and the fraction \frac{2}{8}depicts the specific portion we have chosen.
Fraction of a Collection
Fraction of a collection represents the number of equal parts from a collection of objects that we choose.
Let us consider a box of colorful marbles. Among the marbles, six are red and four are blue. The fraction of red marbles within the collection is \frac{6}{10}, as there are six red marbles out of a total of ten marbles. Similarly, the fraction of blue marbles is \frac{4}{10}. These fractions give a clear representation of the proportion of each type of marble within the collection.
Fractions on a Number Line
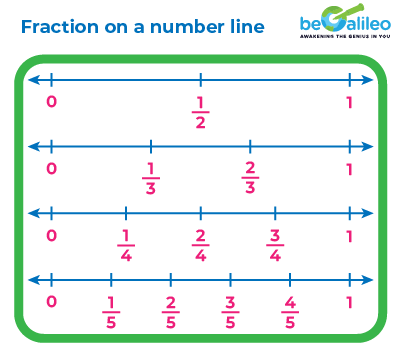
Like numbers, fractions can also be placed on the number line. Visualizing fractions on a number line offers insights into their magnitudes. When plotted, fractions help us understand their relationships to whole numbers and other fractions, providing a visual representation of their sizes.
By dividing the number line into equal portions, typically from 0 to 1, fractions can be accurately depicted. The denominator of the fraction designates the count of divisions on the number line. For instance, to illustrate \frac{1}{5}, the number line is divided into five equal parts from 0 to 1. The initial division marks \frac{1}{5}, followed by \frac{2}{5},\frac{3}{5}, and \frac{4}{5}. Notice that the final interval is \frac{5}{5}, signifying 1 as the whole.
Below, observe a visual representation of these fractional points on a number line.
Types of fractions
Based on the numerator and denominator, fractions can be classified into different types, which are listed below-
Proper Fractions
A fraction where the numerator is always smaller than the denominator is called a proper fraction.
Example: \frac{3}{4} is a proper fraction.
Improper Fractions
A fraction where the numerator is always greater than or equal to the denominator is called an improper fraction.
Example: \frac{5}{4} is an improper fraction.
Mixed Fractions
A mixed fraction is a fraction that is a combination of two numbers, whole number and a proper fraction.
Example: 1\frac{1}{4} is a mixed fraction.
Unit Fractions
A unit fraction is the one where the numerator is always 1.
Example: \frac{1}{4} and \frac{1}{7} are unit fractions.
Like Fractions
Like fractions are the fractions where the denominator is the same.
Example: \frac{1}{4},\frac{3}{4} and \frac{5}{4} are like fractions.
Unlike Fractions
Unlike fractions are the fractions whose denominator is not the same.
Example: \frac{1}{3},\frac{3}{4} and \frac{5}{7} are unlike fractions.
Equivalent Fractions
Equivalent fractions are the fractions which have the same value after being simplified or reduced.
Example: \frac{1}{2},\frac{2}{4} and \frac{4}{16} are equivalent fractions.
| Type of Fraction | Distinct Attribute | Example |
|---|---|---|
| Proper Fraction | Numerator < Denominator | \frac{2}{5} |
| Improper Fraction | Numerator ≥ Denominator | \frac{7}{4} |
| Mixed Fraction | Whole + Proper Fraction | 3\frac{1}{2} |
| Unit Fraction | Numerator = 1 | \frac{1}{9} |
| Like Fractions | Same Denominator | \frac{3}{7},\frac{5}{7},\frac{6}{7} |
| Unlike Fractions | Different Denominators | \frac{2}{5},\frac{3}{8},\frac{7}{11} |
| Equivalent Fractions | Represent Same Value | \frac{1}{2},\frac{2}{4},\frac{3}{6} |
Real-world Application of Fractions
Just like whole numbers, fractions too are very useful in day to day life. Here's a glimpse of how fractions come into play in the real world:
- Cooking and Baking : Recipes often call for fractions to achieve precise measurements of ingredients, from adding \frac{1}{4} teaspoon of salt to \frac{3}{4} cup of flour.
- Measurement : Lengths, areas, and volumes are frequently expressed as fractions, ensuring accuracy in carpentry, construction, and engineering.
- Currency and Finance : Fractions are integral in handling money, understanding interest rates, and calculating discounts.
- Medical Dosages : Accurate medication dosages, often in fractional units, are essential in healthcare to ensure patient safety.
- Art and Design : In art, fractions guide the placement of elements and proportions, while designers use fractions to create layouts.
- Sports and Fitness : Fractions determine sports statistics, such as scoring percentages in basketball or calculating BMI (Body Mass Index).
- Music : Musical notes and rhythms are expressed as fractions, dictating the duration and timing of sounds.
In essence, fractions are everywhere, enriching our understanding of quantities, proportions, and divisions in the world around us.

Solved Examples
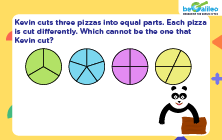
Q1. Choose the shape whose shaded portion represents the fraction \frac{2}{7}.
Solution:
The correct answer is b)
\frac{2}{7}
represents the fraction.
when a whole is divided into 7 equal parts in which 2 are shaded.
Q2. Which of these is a unit fraction?
Solution:
The correct answer is d) \frac{1}{5}
Fractions with numerator 1 are called unit fractions.
So,\frac{1}{5}is a unit fraction.
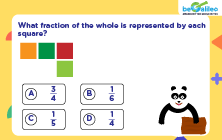
Q3. Choose the improper fraction from the given list of fractions.
Solution:
The correct answer is c) \frac{5}{3}
An improper fraction is a fraction in which the numerator is greater than the denominator.
Numerator = 5
Denominator = 3
5 > 3
So,\frac{5}{3} is an improper fraction.
Q4. If the given fractions are equivalent, then find the values of a and b. \frac{3}{5},\frac{6}{a} and \frac{12}{b}
Solution:
The correct answer is d) a = 10 and b = 20
\frac{3}{5}=\frac{6}{a}=\frac{12}{b}
\frac{3}{5}=\frac{3\times2}{5\times2}=\frac{6}{10}
\frac{6}{10}=\frac{6}{a}
a = 10
\frac{3}{5}=\frac{3\times4}{5\times4}=\frac{12}{20}
\frac{12}{20}=\frac{12}{b}
b = 20
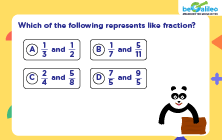
Q5. If two fractions are like fractions, then which of these can never be true about the fractions?
Solution:
The correct answer is d) Both are unit fractions.
Like fractions are fractions that have the same denominator. Proper and Improper fractions can have the same denominator but two distinct unit fractions will always have different denominators.
Practice Problems
FAQs - Fractions
What is a fraction?
A fraction is a mathematical representation of a part of a whole or a collection. It consists of a numerator (the top number) that signifies the parts taken and a denominator (the bottom number) that indicates the total parts in the whole or collection.
What are the types of fractions?
Fractions can be classified based on the values of numerator and denominator. The various types of fractions are unit fractions, proper fractions, improper fractions, equivalent fractions, like and unlike fractions.
How do fractions help in real life?
Fractions are essential in real life for various tasks, including cooking measurements, sharing objects equally, understanding time intervals, dealing with money, calculating medication dosages, and more. They offer precise ways to express parts of a whole in diverse scenarios.
Can fractions represent values greater than 1?
Yes, fractions can represent values both less than and greater than 1. Improper fractions and mixed numbers are examples of fractions that can represent values greater than 1. An improper fraction has a numerator equal to or greater than the denominator, and a mixed number combines a whole number and a proper fraction.
Where are equivalent fractions useful?
Equivalent fractions are useful when you want to express the same part of a whole or the same proportion using different numbers. They help in simplifying calculations and comparisons.
Are all fractions less than 1?
No, not all fractions are less than 1. Fractions can represent any portion of a whole, including portions greater than 1. These fractions are called improper fractions or mixed numbers. An improper fraction has a numerator that is equal to or greater than its denominator, such as \frac{5}{4} or \frac{7}{3}. A mixed number is a combination of a whole number and a proper fraction, like 2\frac{1}{2} or 3\frac{3}{4}. Both improper fractions and mixed numbers can represent values greater than 1.
Did you know?
Clocks and watches rely on fractions to mark hours, minutes, and seconds, translating fractions of time into meaningful intervals.