Table of contents
- Definition of Natural Numbers
- Examples of Natural Numbers
- Types of Natural Numbers
- Is 0 a Natural Number?
- Symbol for Natural Numbers
- History of Natural Numbers
- Natural Numbers on a Number Line
- Properties of Natural Numbers
- Predecessor and Successor of a Number
- Solved Examples
- Practice Problems
- Frequently Asked Questions
Since time immemorial, the necessity to count and quantify has driven the evolution of numbers. Natural numbers, our foundational counting numbers, have been instrumental in shaping the landscape of mathematics. These fundamental numbers serve as the building blocks from which mathematical exploration takes its first steps.
Definition of Natural Numbers
Natural numbers are a set of positive integers that begin from 1 and continue infinitely. They do not have any fractional or decimal components.
In other words, Natural numbers are the counting numbers used for basic counting and ordering.
The set of natural numbers includes 1, 2, 3, 4, 5,.... and continue till infinity.
Examples of Natural Numbers
All counting numbers are considered as natural numbers.
Imagine you are counting the number of apples in a basket. As you place each apple into the basket, you start with one apple, then two, then three, and so on. The number of apples you count are natural numbers: 1, 2, 3, and so forth. These numbers represent the quantity of apples you have without considering fractions, decimals, or negative values.

Here are some more examples of natural numbers - 543, 289768 and 8790.
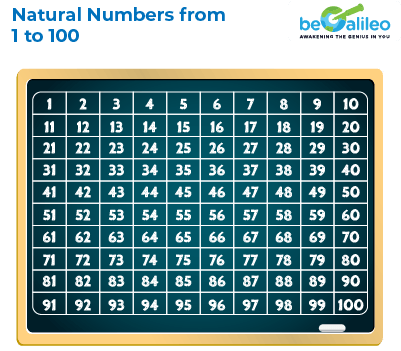
Types of Natural Numbers
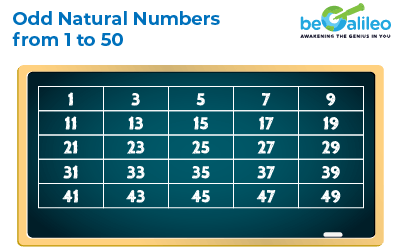
Odd Natural Numbers
Odd natural numbers are positive numbers that are not divisible by 2 and have a remainder of 1 when divided by 2. Here is the list of odd natural numbers from 1 to 50.
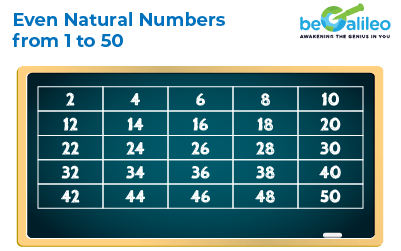
Even Natural Numbers
Even natural numbers are positive numbers that are divisible by 2. Here is the list of even natural numbers from 1 to 50.
Is 0 a Natural Number?
No, 0 is not considered a natural number.
Natural numbers are counting numbers. We do not count something that is not there. For counting there has to be at least one object to count. So, natural numbers start with 1.

Symbol for Natural Numbers
Natural Numbers are represented using a set notation as

It is read as, ℕ is a set of all natural numbers from 1 to infinity.
ℕ is the notation used to represent natural numbers.
{ } is the curly brackets used to denote the set.
∞ is the symbol used to represent infinity.
History of Natural Numbers
The concept of natural numbers has a long and fundamental history in mathematics. Here's an overview of their historical development:
Ancient Civilizations : The earliest known civilizations, such as the ancient Egyptians and Sumerians, had basic systems for counting and representing numbers. They used natural numbers for practical purposes like counting objects, tracking quantities of goods, and measuring time.
Ancient Greece : Greek mathematicians like Pythagoras and Euclid laid the foundation for more systematic study of numbers. Euclid's "Elements," a comprehensive compilation of ancient mathematical knowledge, introduced the concept of Euclidean division algorithm and explored properties of natural numbers.
Indian Mathematics : Indian mathematicians, particularly in the Vedic period and thereafter, made significant contributions to number theory. They developed systems of notation, introduced the concept of zero, and delved into divisibility properties and prime numbers.
Arabic Mathematics : During the Islamic Golden Age, Arabic mathematicians preserved and extended the knowledge of ancient Greece and India. Al-Khwarizmi's work on arithmetic and algebra furthered understanding of natural numbers and their manipulation.
Number Theory : In the 17th and 18th centuries, mathematicians like Fermat and Euler contributed to number theory, exploring properties of prime numbers and divisibility, laying the groundwork for deeper insights into natural numbers.
Throughout history, natural numbers have been essential for practical tasks, intellectual exploration, and the development of various mathematical theories. They form the basis for arithmetic, number theory, and many other branches of mathematics, and their significance continues to be recognized in modern research and education.
Number Line Representation
The number line is a visual representation of numbers where each point corresponds to a unique number.
For natural numbers, the number line starts at 1 and extends infinitely to the right.
For example, a set of natural numbers from 1 to 10 is represented on the number line as pictured.

- The number 1 is the starting point of the number line.
- The numbers increase as you move to the right along the line: 2, 3, 4, and so on.
- There is no specific endpoint to the right – natural numbers continue infinitely.
It's important to note that zero (0) is not included in the representation of natural numbers on the number line, as zero is not considered a natural number.
Properties of Natural Numbers
Natural numbers have several important properties that form the foundation for various mathematical concepts and operations. Here are some key properties of natural numbers:
Counting and Cardinality: When calculating the cardinality (size) of finite sets, one uses natural numbers to count and describe the value. If a set contains n elements, where n is a natural number, this means that it can be compared one-to-one to the set of natural numbers from 1 to n.
No Zero or Negative Numbers: Natural numbers do not include zero or negative numbers; they begin at 1 and go upward.
Closure under Addition and Multiplication: When you add or multiply two natural numbers, the result is always a natural number. For example, if you add 5 and 8, you get 13, which is also a natural number.
Associative and Commutative Properties: Addition and multiplication of natural numbers are associative (changing the grouping of numbers doesn't change the result) and commutative (changing the order of numbers doesn't change the result).
Distributive Property: Multiplication distributes over addition for natural numbers, meaning a(b + c) = ab + ac.
Well-Ordered: Natural numbers have a natural order: 1 comes before 2, 2 comes before 3, and so on. This property is known as well-ordering.
No Maximum Element: Natural numbers do not have a maximum element. No matter how large a natural number you have, you can always find a larger one.

Predecessor and Successor of a Natural Number
Predecessor:
The predecessor of a natural number 'n' is the natural number that comes immediately before 'n' in the sequence of natural numbers.
For example:
The predecessor of 5 is 4.
The predecessor of 1 is not defined in the context of the natural numbers because there's no natural number that comes before 1.
Successor:
The successor of a natural number 'n' is the natural number that comes immediately after 'n' in the sequence of natural numbers.
For example:
The successor of 3 is 4.
The successor of 0 is 1.
Solved Examples
Q1. Which of the following is not a natural number?
Solution:
The correct answer is b) 2 × 5 – 5 × 2
2 × 5 – 5 × 2 = 0 is not a natural number, as natural numbers are positive numbers starting from 1 and do not include zero.
Q2. Find the sum of the first 5 natural numbers.
Solution:
The correct answer is 15.
The first 5 natural numbers are 1, 2, 3, 4, and 5.
Thus, Sum = 1 + 2 + 3 + 4 + 5 = 15
Q3. The smallest and greatest 7-digit number using 7, 0, 3 and 1 is ____ and _____.
Solution:
The correct answer is 1000037 and 7777310
The smallest 7-digit number that can be formed using the digits 7, 0, 3, and 1 is 1000037.
The greatest 7-digit number that can be formed using these digits is 7777310.
Q4. Choose the predecessor of natural number 1 .
Solution:
The correct answer is d) Does not exist
The concept of a predecessor involves finding the number that comes immediately before a given number.
However, for the natural number 1, there is no natural number that comes before it, as natural numbers start from 1 and continue upwards.
Thus, the predecessor of the natural number 1 does not exist.
Q5. Find the number of seconds in a week.
Solution:
The correct answer is 604,800 seconds in a week
To find the number of seconds in a week, you can calculate:
Number of seconds in a week = Number of seconds in an hour × Number of hours in a day × Number of days in a week
Number of seconds in a week = 3600 × 24 × 7 = 604,800 seconds
So, there are 604,800 seconds in a week.
Q6. Find the TRUE statement.
Solution:
The correct answer is c) The natural numbers are the counting numbers.
Natural numbers do not include fractions or decimals. They do not include negative numbers. They continue indefinitely without any upper limit.
Natural numbers, often called "counting numbers," are the set of positive integers that are used for counting and ordering.
Practice Problems
FAQs - Natural Numbers
What are natural numbers?
Natural numbers are a set of positive integers used for counting and ordering. They start from 1 and continue indefinitely (1, 2, 3, ...).
Is 0 a natural number?
No, 0 is not considered a natural number. Natural numbers start from 1, and zero is not included in this set.
What is the smallest natural number?
The smallest natural number is 1.
Are all natural numbers positive?
Yes, all natural numbers are positive. Natural numbers are a set of integers used for counting and ordering, starting from 1 and going upward (ie 1, 2, 3, ...). They do not include negative numbers or zero.
Is every natural number a whole Number?
Natural numbers start from 1 and continue indefinitely (1, 2, 3, ...), while whole numbers include both natural numbers and zero (0, 1, 2, 3, ...). In other words, every natural number is a whole number, but not every whole number is a natural number.
What are the first 5 natural numbers?
The first 5 natural numbers are: 1, 2, 3, 4, 5.
Is 4.8 a natural number?
The number 4.8 is a decimal number and is not considered a natural number.
Can natural numbers be negative?
No, natural numbers are only positive numbers. They do not include negative numbers.
What is the difference between natural numbers and whole numbers?
Natural numbers start from 1, while whole numbers start from 0. Whole numbers include both natural numbers and zero (0, 1, 2, 3, ...).
What is the sum of n natural numbers?
The sum of the first n natural numbers is given by the formula:\frac{n(n+1)}{2}
What is the successor of a natural number?
The successor of a natural number ‘n’ is the next natural number, which is obtained by adding 1 to n.
How are prime numbers related to natural numbers?
Prime numbers are natural numbers greater than 1 that have only two positive divisors: 1 and themselves. Examples include 2, 3, 5, 7, 11, and so on.
Can a natural number be both even and prime?
No, except for the number 2, all prime numbers are odd. This is because an even number greater than 2 can always be divided by 2, and therefore cannot have only two divisors.









