Table of contents
Exploring Prime Numbers: Unlocking the Beauty of Mathematics
Numbers are incredibly fascinating, with numerous ways to interpret and analyze them. Let's delve into the captivating realm of prime numbers and uncover the secrets they hold.
What are Prime Numbers?
Prime numbers are special numbers that possess unique properties in mathematics. They have only two factors: 1 and the number itself. For example, the numbers 5 and 7 are prime numbers, as they can only be divided evenly by 1 and themselves.

Prime numbers are the building blocks of the number system, playing crucial role in various mathematical concepts and calculations. They have fascinated mathematicians for centuries due to their elusive nature and intriguing patterns.
Understanding Prime Numbers with Visual Models
The concept of prime numbers is fascinating and can be explored through simple visualizations. Let's consider a scenario with marbles to understand it better.

Imagine you have 5 marbles. How many different ways can you arrange them in equal groups?
By carefully examining the marbles, you'll notice that there are only two ways to arrange them: you can either keep all 5 marbles together as a single group or separate them into individual groups of 1 marble each.

Now, let's consider another scenario with 7 marbles. Similarly, in how many ways can you arrange them in equal groups?
Upon observation, you'll find that again there are only two ways: keeping all 7 marbles together or arranging them into individual groups of 1 marble each.
Through these simple examples, we can observe that certain numbers have a unique property of having exactly two factors: 1 and the number itself. In other words, prime numbers are not divisible by any other number except 1 and itself. For instance, the numbers 2, 3, 5, and 7 are prime numbers because they satisfy this criterion.
The Significance of Prime Numbers
Prime numbers hold a significant place in the world of mathematics. They are the fundamental building blocks from which other numbers emerge through multiplication.
Understanding prime numbers helps us comprehend the structure and patterns within the realm of numbers. Prime numbers find extensive applications in number theory, cryptography, and algorithms. Their unique properties make them essential in modern encryption methods used to protect sensitive information from cyber-crimes.
The History of Prime Numbers
The exploration of prime numbers dates back to ancient times. Greek mathematician Euclid mentioned prime numbers in his work 'Elements,' recognizing their importance and studying their properties. However, it was another Greek mathematician, Eratosthenes, who made significant contributions to understanding prime numbers.
Eratosthenes invented the renowned "Sieve of Eratosthenes" algorithm, which aids in identifying prime numbers. This method, developed over two thousand years ago, is still widely used today.
However, it was not until the 17th century that mathematicians like Fermat, Euler, and Gauss began to examine the structure within prime numbers.
The Sieve of Eratosthenes
Let's explore the Sieve of Eratosthenes, a method developed by Eratosthenes, to identify prime numbers between 1 and 100.
The Sieve of Eratosthenes works by systematically crossing out composite numbers, leaving only the prime numbers behind. Here's how it works:
Step 1: Begin by listing all numbers from 1 to 100.

Step 2: Start with the first prime number, which is 2. Circle it and cross out all multiples of 2, excluding 2 itself.

Step 3: Move to the next available number, which is 3. Circle it and cross out all multiples of 3, excluding 3 itself.
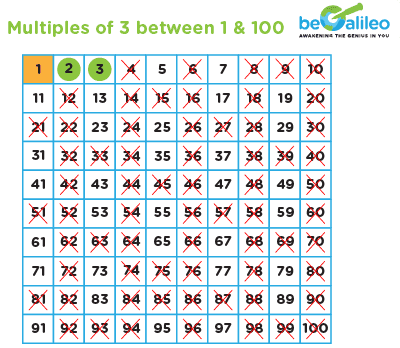
Step 4: Repeat the process with the remaining prime numbers (5, 7, 11, etc.), circling them and crossing out their multiples
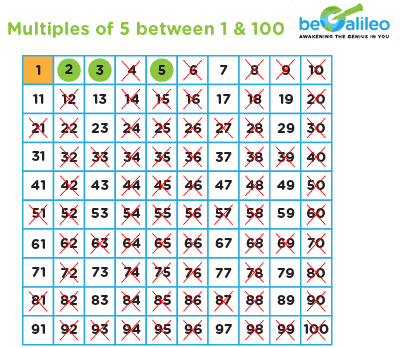
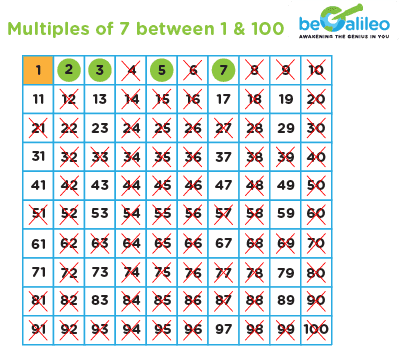
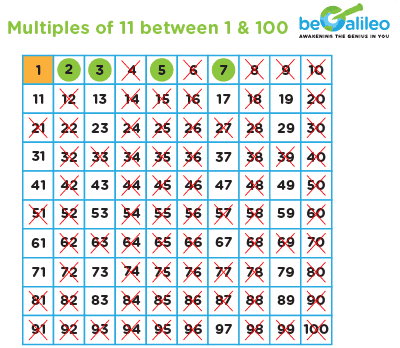
Step 5: Continue this process until you reach the end of the number grid.

The circled numbers that remain are the prime numbers between 1 and 100, as determined by the Sieve of Eratosthenes.
Prime Numbers Chart 1 to 100
A prime numbers chart systematically represents all prime numbers from 1 to 100. Prime numbers, except for 2, are odd numbers. The chart below lists all the prime numbers from 1 to 100

Twin Prime Numbers
Twin prime numbers are a fascinating and intriguing concept within the realm of prime numbers. Twin primes are pairs of prime numbers that differ by 2. In other words, they are prime numbers that have a difference of only 2 between them. For example, (3, 5), (5, 7), (11, 13), and (17, 19) are all examples of twin prime pairs.

Difference between Co-Prime Numbers and Prime Numbers
Co-prime numbers, also known as relatively prime or mutually prime numbers, is an interesting concept in mathematics. Two numbers are considered co-prime if their greatest common divisor (GCD) is 1. In other words, there is no common factor other than 1 between them.
For instance, let's take the numbers 8 and 15. The factors of 8 are 1, 2, 4, and 8, while the factors of 15 are 1, 3, 5, and 15. The only common factor between them is 1. Therefore, 8 and 15 are co-prime numbers.
It's important to note that co-prime numbers do not have to be prime numbers themselves. For example, 10 and 21 are co-prime numbers because their only common factor is 1, even though neither of them is a prime number.
To summarize, Co-prime numbers have only one common factor, which is the number one. On the other hand, prime numbers have two common factors: 1 and the number itself.
Interesting Facts about Prime Numbers
Prime numbers hold intriguing characteristics and have various real-world applications. Here are some interesting facts about prime numbers:
- Divide the numerator (the top number) by the denominator (the bottom number).
- Perform the division, keeping track of the quotient and any remainders. Continue the division until you reach your desired level of decimal precision or until the remainder becomes zero, indicating that the division is complete.
- The result you obtain from the division is the decimal representation of the fraction.
Solved Examples
Q1. Which of the following numbers is a prime number?
- a) 15
- b) 17
- c) 22
- d) 27
Solution: The correct answer is b) 17.
It is a prime number as it is only divisible by 1 and 17 itself.
Q2. What is the smallest prime number?
- a) 1
- b) 2
- c) 3
- d) 4
Solution: The correct answer is b) 2.
It is the only even prime number and the smallest prime number.
Q3. Which of the following numbers is not a prime number?
- a) 11
- b) 15
- c) 19
- d) 23
Solution: The correct answer is b) 15.
It is divisible by 3 and 5, so it is not a prime number.
Q4. How many prime numbers are there between 20 and 30?
- a) 2
- b) 3
- c) 4
- d) 5
Solution: The correct answer is a) 2.
The prime numbers between 20 and 30 are 23 and 29.
Q5. Is 1 a prime number?
- a) Yes
- b) No
Solution: The correct answer is b) No.
1 is not considered a prime number as prime numbers are defined to have exactly two distinct positive factors.
Q6: Which of the following numbers are prime?
- a) 3
- b) 9
- c) 47
- d) 39
Solution: The correct answer is a) and c).
The only factors in a prime number are 1 and itself.
The factors of 3 are 1 and 3. Since the only factors in 3 are 1 and itself, 3 is prime.
The factors of 9 are 1, 3, and 9. Since 9 has more factors than just 1 and itself, 9 is not prime.
The factors of 47 are 1 and 47. Since the only factors in 47 are 1 and itself, 47 is prime.
The factors of 39 are 1, 3, 13, and 39. Since 39 has more factors than just 1 and itself, 39 is not prime.
The prime numbers are 3 and 47.
Practice Problems
1. Which of these is a prime number?
8
13
16
1
2. Max says all the odd numbers are prime numbers, and Mia says if the factors of the number are 1 and the number itself, then it is a prime number. Who is correct?
Max
Mia
Both of them
None of them
3. Which of the following numbers is not prime?
57
47
61
59
4. Look at the pattern given below and choose the next two numbers to complete the prime sequence. 11, 13, 17, 19, 23, ___, ___
24,25
29, 31
31, 37
27, 29
5. How many prime numbers are there between 40 and 60?
6
3
7
5
6. Consider the following expression: 60 × 15 + 52 + 43.
Amy claims that the expression gives a prime number.
Is she correct? Why or Why not?
Yes, because all the numbers are prime.
No, because the number is a multiple of 5.
No, because the sum of prime numbers is an odd number.
None of the above.
Frequently Asked Questions
What age group is beGalileo designed for?
Can I try beGalileo before committing to a package?
What is the difference between self-paced and live class options in beGalileo?
How can beGalileo support homeschooling parents?
What curriculum does beGalileo follow?
How can I track my child's progress?
What is the frequency and duration of beGalileo tutoring classes?
Can beGalileo's program be customized for my child's specific learning requirements?
Can your teachers teach topics covered in my child's school curriculum?
Can my child join beGalileo anytime during the year?
What if I am not satisfied with beGalileo's classes after enrolling?
How do I enroll for beGalileo's classes?



Did you know?
The number zero (0) is neither positive nor negative and is considered an important mathematical concept.






