The Derivative Calculator is a powerful online tool designed to calculate and simplify the process of finding derivatives. The derivative calculator deals with complex derivatives, a fundamental concept of calculus.
In mathematics, a derivative is a concept from calculus that represents the rate at which a function's value changes as its input changes.
When graphed, the derivative at a specific point corresponds to the slope of the tangent line to the function's curve at that point. This slope indicates how steeply the function is increasing or decreasing at that precise location.
Derivatives have numerous applications. They are used to solve problems involving rates of change in various fields such as physics, engineering, economics, and biology. In practical terms, derivatives can help determine the speed of a moving object, the rate of reaction in chemistry, the marginal cost in economics, or the rate of growth in a biological population, among other examples.
How to use the derivative calculator?
Input
Enter the mathematical function for which you want to find the derivative.
Make sure that your function is correctly formatted and uses the variable ‘x’ in the function.
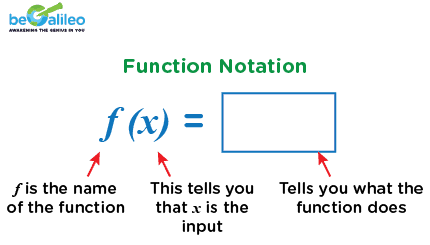
The calculator supports a wide range of functions, including polynomial, trigonometric, exponential, and logarithmic functions.
Calculation
Click “CALCULATE”and the first derivative of the given function will be shown.
Reset
Click on “RESET” to start with the new calculation to avoid computing errors in the new calculation.
How to find the derivative of a function?
The derivative is a fundamental concept in calculus that provides a precise way to understand how the values of functions change when their input values change.
There are some general rules followed for the derivation.
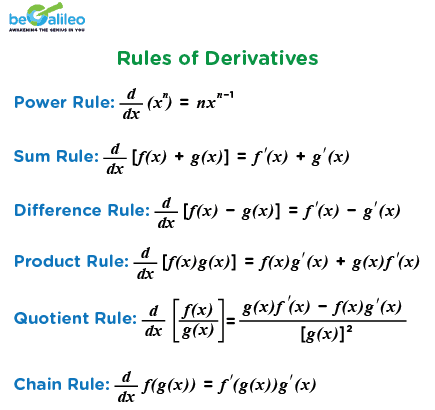
We also have some special functions and their derivatives. They can be tabulated as:
\text{Example : Find the derivative of} \quad {3x^2 +2x}
\text{Let f} = \quad {3x^2 \quad and \quad g=2x}
\text{Then,f} = \quad {3(2x) \quad =6x \quad and \quad g =2(1)}
{f^' + g^' = 6x+1}
\text{So,} f\left(3x^2 + 2\right)= {6x \quad + 1}
Solved Examples
1.Find the derivative of \quad \frac{sin^2x} {e^x}.
f = \quad {sin^2x} \quad\text{and} \quad{g \quad= \quad e^x}.
We can use the quotient rule \frac {f} {g} = \frac{f'g'- g'f'}{g^2}
f=2 sinx cosx and g= e^x
\frac{f'}{g'} = \frac {2sinx cosx \quad e^x -e^x sin^2x}{e^{2x}}
So, f'(x)= \frac {2sinx cosx \quad e^x -e^x sin^2x}{e^{2x}}
2.Find the derivative of \quad-8x^2+53x-6
let,f= \quad-8x^2+53x-6
let,f'= \quad-2(8x)+53(1)+0
f'= \quad -16x+53
So,f'= \quad -16x+53
Frequently Asked Questions
1)What types of functions does the calculator support?
Our calculator supports a wide range of functions: polynomials, trigonometric, exponential, and logarithmic in calculus.
2)Why is the derivative important?
Derivatives play an important role in calculus and find widespread application across disciplines such as physics, engineering, economics, and biology. Derivatives offer an understanding of how different quantities vary over time in relation to other variables.
3)How is the derivative denoted?
The derivative of a function f(x) is often represented as dfdx or f'(x) or f' .
4)Can derivatives be negative?
Yes, derivatives can be negative. A negative derivative indicates that the function is decreasing at that point. A positive derivative means that the function is increasing at the given point.
5)What information can we get about a function from its derivative?
The derivative provides information about the rate at which a function is changing. It gives the slope of the tangent line to the curve at a specific point.
6)What are the rules involved in finding the derivative of a function?
The rules involved in derivatives of a function are power rule, product rule, quotient rule, and chain rule.
