What if you are told that nature’s architect is mathematics? What if you become aware of the fact that musical note poetry has something to do with numbers? Does it surprise you? Don’t be surprised if you come across many more amazing things about a collection of numbers called “The Fibonacci Numbers.” Let us read on and learn more about them.
What is Fibonacci number?
Leonardo Pisano made the initial discovery of the Fibonacci sequence. The name “Fibonacci” came from his nickname as he was commonly known by it. The special pattern followed by these numbers is as follows: “Each number in the collection is equal to the sum of the two numbers that came before it.”
These numbers were first introduced by an Indian Sanskrit poet by the name “Hemachandra.” But Fibonacci was the first to record these numbers in his book by name “Liber Abaci.” In the book he posed it as a question that involves rabbit reproduction. The question said “ If a newly born pair of rabbits (male and female) are put in a field. The rabbits are ready to mate after a month so that at the end of the second month they can produce another pair of rabbits. Assuming that the female never dies and keeps producing a new pair every month from the second month on. How many pairs will be there in a year?”
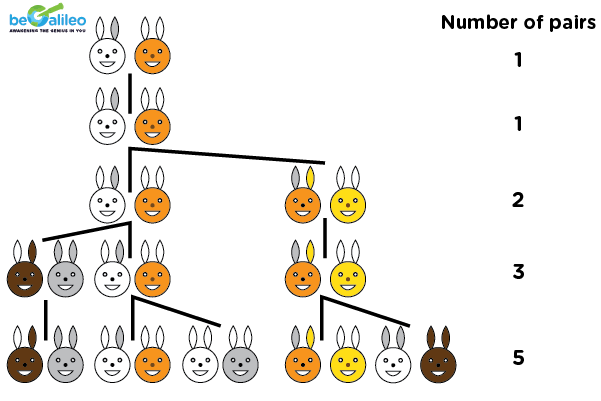
If we put the number of pairs present in the field each month then, we get:
1, 1, 2, 3, 5, 8, 13, 21, 34, ……..
This is a collection of the Fibonacci numbers. Though the rabbit story sounds a little unreal, people can connect to it as an understandable notion.
Unlock Your Child's Math Potential with beGalileo!

🚀 Transform their math skills with personalized, 1-on-1 classes.
🧮 Experience integrated math and coding for real-world application.
👦 See your child excel—start with a Free Trial Math Class today!
What is special about these numbers?
These numbers act as the building blocks of beauty in nature’s architecture. Not only that, these numbers are used to fill in missing notes in a piece of music and also establish the ratio of beauty.
Fibonacci Numbers In Flowers
The seeds on a sunflower’s head are arranged in a certain manner to adhere to the Fibonacci sequence. This spiral helps sunflower seeds survive by preventing them from crowding one another out.
Have you ever counted the number of petals on a lily, Shasta Daisy, or Corn Marigold? If we did, we would have come to know the amazing fact that the number of petals on these flowers is always one of the Fibonacci numbers. Not just these flowers, here is a list of the Fibonacci flowers.
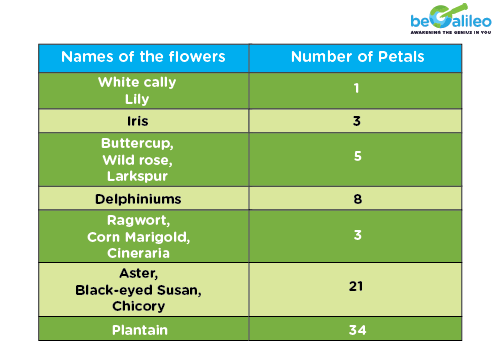
Go on and count the number of petals of the flowers whose pictures are given below and get amazed more!




There are more facts about these numbers to leave us awestruck. The arrangement of seeds on flower heads contains Fibonacci numbers. The number of spirals in some flower heads is again a Fibonacci number.
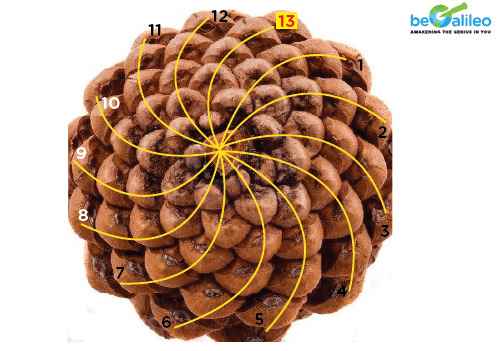
In a cauliflower, you can see the Fibonacci spiral.

Bananas and Pineapples also include the Fibonacci numbers. Bananas have three or five flat sides, and pineapple scales include sets of eight, thirteen, and twenty-one Fibonacci spirals.


So, the next time you gulp a banana or a pineapple, remind yourself that you are eating numbers!
Fibonacci Series Numbers in organs of a Human body
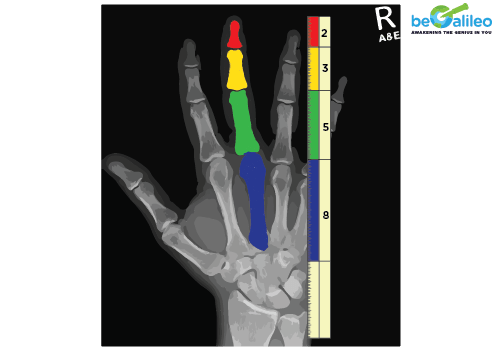
Here is another Fibonacci number example. Every human being has 2 hands, each of which has 5 fingers and 3 sections, divided by 2 knuckles.. What are 2, 5, 3 again? They are the Fibonacci numbers!
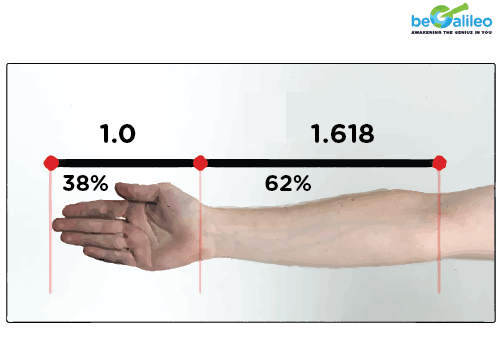

Our inner ear also forms a Fibonacci spiral.

Fibonacci Numbers in Music
This concept of musical notes was originally introduced in Sanskrit poetry by an Indian poet by name “Hemachandra.” To fill any musical note, we use a combination of a short syllable or a long syllable. As an instance of tabla, short syllables can be “Dhina,” whereas the long syllable can be “TaDiGina.” Suppose I say that we have a musical note with 5 notes missing. How many combinations of the long and the short syllables will you be needing to fill it? We will be needing the 5th Fibonacci number of combinations of the two syllables to fill the musical note. These combinations play an important role in the way the music sounds. A harmonious combination is always a combination coming out of the Fibonacci numbers series.
The Golden Ratio ∅
Represented by the Greek letter Phi ( ∅ ) =1.6180339887. How did the beauty ratio or the golden ratio 1.6180339887…… come from?
Let us see the calculations that generates the Golden Ratio.
Calculation:
1/1 = 1
2/1 = 2
3/2 = 1.5
5/3 = 1.666
8/5 = 1.6
13/8 = 1.625
21/13 = 1.61538
34/21 = 1.61905
55/34 = 1.61764
89/55 = 1.61861
144/89 = 1.61798
233/144 = 1.61806
If we continue the procedure we will generate the “Golden Ratio ∅ (phi).” We find this (phi) in world famous arts and architecture.

Example 2: It is located in Egypt’s great pyramid. ∅ is equal to the pyramid’s perimeter divided by twice its vertical height.
Example 1: In the Monalisa Painting by Leonardo Da Vinci.

MatheMagic
We have generated the Fibonacci clock for you!
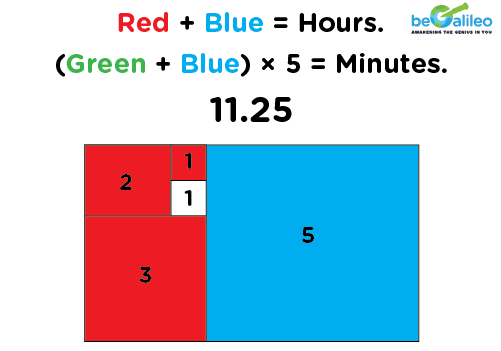
Can you tell the time now using the Fibonacci Clock?
Interesting Applications
1. Miles to km conversion
Take any two consecutive numbers from the set of Fibonacci numbers. For instance say 13 and 21 or 34 and 55.
Now, if the smaller number in miles is equal to the other one in km or vice versa.
i.e. 34 Miles = round (54.72) Kilometers = 55 Kilometers
21 Kilometers = round (13.05) Miles = 13 Miles
2. In Cryptography
These numbers and the pattern is used as a key to encrypt and decrypt codes. This is one of the efficient ways to increase cyber security.
2. In Cryptography
These numbers and the pattern is used as a key to encrypt and decrypt codes. This is one of the efficient ways to increase cyber security.
3. In Stock Market
The stock market is where Fibonacci numbers sequence are used in another important way. The “Fibonacci Retracement Levels,” which are based on the Fibonacci sequence, are used by traders in this industry. These percentages typically involve 23.6%, 38.2%, 61.8%, and 78.6%. In real life, traders can develop a retracement indication by comparing a high point to a low point utilizing the Fibonacci Retracement Levels. Then, these Levels might tell us if a price is likely to bounce back or stall.
Conclusion
Nevertheless, Fibonacci Numbers play a prominent role in our lives and we can say it is a part and parcel of every living being. As the poem says:
" The sun is gone at sunset,
The sunrise has not disappointed us yet.
The moon is in sight every night,
Part or Full never out of sight.
Changing tides of the oceans,
With the rising and falling motions.
Nature is the house of patterns,
Amazing you like magic Lanterns.
This amazing magic lantern is the “Fibonacci Pattern.” Just like Francis Bacon says “ Beauty by itself is the sensible image of the infinite,” we discovered the spell bounding infinite series of numbers defining beauty all around us.
